Tri par arbre binaire de recherche
Présentation
Le tri par Arbre Binaire de Recherche est un tri classé à part, non pas parce qu’il est plus performant, mais parce qu’il nécessite quelques connaissances sur une structure particulière appelée "arbre". Un arbre est une structure composée d’une racine et plusieurs pointeurs vers d’autres arbres ou vers une feuille. Une feuille est un arbre particulier qui ne possède aucun sous arbre, c’est un arbre terminal. Un noeud est la racine d’un sous arbre. L’exemple ci-dessous illustre le vocabulaire qui viens d’être décrit.
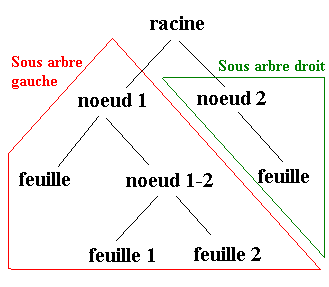
Dans les tris précédents, nous avons déja eu l’occasion de manipuler une structure de type "arbre". Il s’agit des listes, qui sont une forme d’arbre particuliére puisque chaque noeud n’est rattaché qu’à un seul sous arbre : une liste est une structure comportant une valeur et un pointeur vers une autre liste.
Les arbres qui nous intéressent ici sont appelés arbres binaires de recherches (ou ABR). "binaire" car ils ne peuvent posséder que deux sous arbres et "de recherche" car les valeurs situées dans le sous arbre gauche d’un ABR sont toutes inférieures à la valeur du nœud de l’arbre, et celles situées dans le sous arbre droit lui sont supérieures. Construction de l’arbre binaire de recherche :
Pour réaliser ce tri il faut tout d’abord construire l’arbre binaire de recherche correspondant aux éléments à classer. C’est ce qui va être fait ici. La première valeur de l’ensemble fera office de racine. Ensuite, pour construire l’arbre binaire, il faut descendre dans l’arbre en comparant les différents éléments à la racine.
Soit l’ensemble à classer suivant :
| 6 | 8 | 3 | 1 | 4 | 9 | 2 | 7 | 5 |
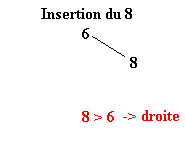
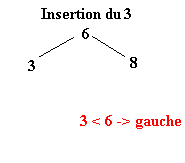
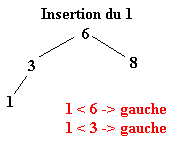
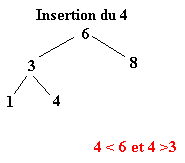
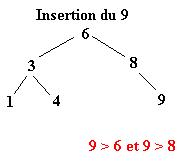
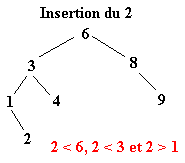
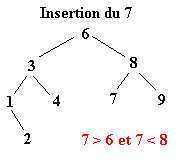
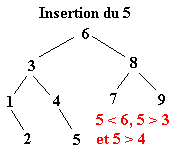
Une fois l’ABR construit, il n’y a plus qu’à exploiter l’une de ses propriétés pour trier l’ensemble des éléments. Il suffit d’effectuer le parcours infixe de l’arbre. Le parcours infixe consiste à visiter récursivement le sous arbre gauche d’un arbre, puis de concaténer le nœud de l’arbre avant de visiter le sous arbre droit. Soit le parcours suivant ou chaque arbre est définit par le numéro de sa racine :
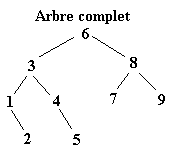
Parcours 6
(Parcours gauche 3) + 6 + (Parcours droit 8)
( (Parcours gauche 1) + 3 + (Parcours droit 4) ) + 6 + ((Parcours gauche 7) + 8 + (Parcours droit 9))
( (1 + (Parcours droit 2)) + 3 + ((4 + (Parcours droit 5)) ) + 6 + ((7) + 8 + (9))
( (1+ (2)) + 3 + ((4 + (5)) ) + 6 + ((7) + 8 + (9))
A l’issu de ce parcours, l’ensemble des éléments est récupéré, et il est classé.
A propos du code source
Dans le cas du code source en Caml et Ocaml, le tri est intégralement présenté ici, le système de programmation par filtrage permettant d’implémenter très facilement des structures récursives comme les arbres. Dans le cas du code source en Java et en C, un fichier externe, disponible en téléchargement, comporte les fonctions élémentaires de création et de manipulation des arbres binaires.
| Pseudo langage | |||||||
| Caml | Java | OCaml | |||||
| Caml (listes) | OCaml (listes) | ||||||
Complexité
Pour parcourir l’arbre binaire de recherche, la complexité est proportionnelle à la taille de l’arbre, c’est à dire le nombre d’éléments que l’arbre contient. Soit une complexité en O(n) où n est le nombre d’éléments à classer.
Pour construire l’arbre binaire de recherche, il faut insérer les n éléments un à un dans un arbre initialement vide. Dans le pire des cas, l’arbre va se construire sous forme d’une liste (arbre filiforme), c’est le cas, par exemple, lorsque l’ensemble des valeurs est initialement classé à l’envers. Dans ce cas, pour classer le pième élément, il faut effectuer (p-1) comparaisons. Soit une complexité T(n) donnée par la formule suivante :
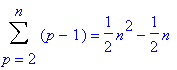
Ce qui correspond à une complexité dans le pire des cas en O(n2).
Dans le meilleur des cas, la complexité de ce tri est heureusement bien meilleure. Par contre, elle est un peu plus compliquée à calculer. Le meilleur des cas correspond au cas ou l’arbre est complet une fois construit. Cela correspond à un arbre de hauteur h et dont toutes les branches de profondeur (h-1) possèdent un arbre droit et un arbre gauche. Tous les nivaux de l’arbre sont donc bien remplis. Dans ce cas l’arbre est capable de stocker le nombre d’éléments suivant :
| Profondeur | Nombres d’éléments stockés |
| 0 | 1 |
| 1 | 1+2 = 3 |
| 2 | 1+2+4 = 7 |
| j | 1+2+4+23+...+2j |
Quand le jième niveau est rempli, il y a donc le nombre d’éléments suivant dans l’arbre :
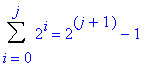
Dans le meilleur des cas, pour insérer le pième élément, il faut effectuer le nombre de comparaisons correspondant au nombre de niveaux remplis. Si le pième élément est inséré au niveau j, on a p=2j+1, d’où p-1=2j+1, soit j+1=lg(p-1) avec lg le logaritme népérien en base 2. Soit, pour finir, j=lg(p-1)-1. Ce résultat correspond au nombre de comparaisons pour insérer le pième élément. Pour insérer les n éléments de l’ensemble à classer dans l’arbre, et donc pour construire ce même arbre, il faut effectuer le nombre de comparaisons T(n) suivant :
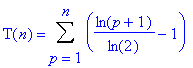
Ce qui se simplifie ainsi :
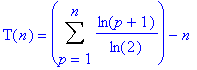
Or, ln(a)+ln(b)=ln(a.b), d’où le résultat suivant :
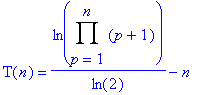
Ce qui s’écrit encore plus simplement :
Il s’agit du calcul exact de la complexité pour construire un arbre binaire de recherche complet à n éléments. Cependant, ce calcul est assez difficile à exploiter : est-ce que ce tri est plus avantageux que les tris vu précédemment ? Nous allons montrer ici qu’il s’agit d’un tri en O(n.ln(n)). Pour cela, il faut montrer l’égalité suivante :
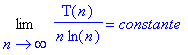
On pose :
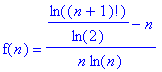
Ce qui se simplifie ainsi :
Or, on a :
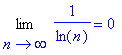
donc, on a :
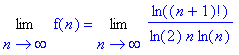
Pour calculer cette limite, il faut en chercher un équivalent à l’infini. Or, d’après la formule de Stirling, on a n ! qui est équivalent à l’infini à :
Soit f(n) qui est équivalent à l’infini à :
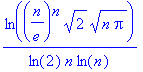
Expression qui se simplifie ainsi :
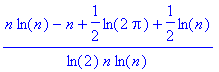
Soit encore :
Or, les trois derniers termes de cette expression tendent de maniére évidente vers 0. D’où le résultat :
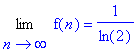
CQFD : C’est ce qu’il fallait démontrer :
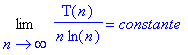
D’où T(n)=O(n.ln(n)), et la complexité de la construction d’un arbre binaire de recherche complet est en O(n.ln(n)).
Conclusion
Le tri par Arbre Binaire de Recherche à les même caractéristiques que le tri rapide. Le seul inconvénient de ce tri est qu’il nécessite la construction d’un arbre binaire de recherche, qui requiert un espace mémoire suffisamment important. Le tri rapide, lui, s’effectue en utilisant l’espace mémoire utilisé par le tableau à trier, il ne nécessite donc pas d’espace mémoire supplémentaire pour construire une nouvelle structure assez compliquée. Le tri fusion, quant à lui, utilise également un espace mémoire important, mais sa complexité en O(n.ln(n)) est garantie, quel que soit l’ensemble à trier.
Accueil des algorithmes de tri
Article précédent : le tri rapide
Article suivant : le tri par casiers
